Man fasse nämlich die beiden Seiten der berandeten
Fläche als Polyederflächen auf, welche längs der
Randcurve (also durchweg unter einem Winkel von 360 Grad)
zusammenstossen und behandele nunmehr statt der ursprünglichen
berandeten Fläche die aus beiden Seiten zusammengesetzte
Gesammtfläche. Diese Gesammtfläche ist dann in der
That eine geschlossene Fläche. Sie ist aber überdiess eine
symmetrische Fläche. Denn wenn man die übereinanderliegenden
Puncte der beiden Flächenseiten vertauscht, so erfährt
die Gesammtfläche eine conforme Abbildung auf sich
selbst mit Umlegung der Winkel. Die Randcurven sind
dabei die Uebergangscurven. Zugleich aber gewinnt unsere
Eintheilung der symmetrischen Flächen in zweierlei Arten eine
wichtige und durchschlagende Bedeutung. Die gewöhnlichen
berandeten Flächen, bei denen man zwei Flächenseiten unterscheiden
kann, entsprechen offenbar der ersten Art. Der
zweiten Art aber correspondiren die Doppelflächen, bei denen
man von einer Flächenseite durch continuirliches Fortschreiten
über die Fläche hin zur anderen gelangen kann. Auch der
Fall ist nicht auszuschliessen (wie bereits angedeutet), dass
die Doppelfläche überhaupt keine Randcurve besitzen mag.
Wir haben dann eine symmetrische Fläche ohne Uebergangscurve
vor uns.
Ich betrachte nunmehr der Reihe nach die verschiedenen
auseinanderzuhaltenden Fälle.
1) Sei zuvörderst eine einfach berandete, einfach zusammenhängende
Fläche gegeben. Eine solche Fläche erscheint für
uns als eine geschlossene Fläche 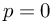 , welche unter Auftreten
einer Uebergangscurve symmetrisch auf sich selbst
bezogen ist. Wir finden also, dass zwei solche Flächen sich
allemal durch Abbildung der einen oder der anderen Art conform
, welche unter Auftreten
einer Uebergangscurve symmetrisch auf sich selbst
bezogen ist. Wir finden also, dass zwei solche Flächen sich
allemal durch Abbildung der einen oder der anderen Art conform
Man fasse nämlich die beiden Seiten der berandeten
Fläche als Polyederflächen auf, welche längs der
Randcurve (also durchweg unter einem Winkel von 360 Grad)
zusammenstossen und behandele nunmehr statt der ursprünglichen
berandeten Fläche die aus beiden Seiten zusammengesetzte
Gesammtfläche. Diese Gesammtfläche ist dann in der
That eine geschlossene Fläche. Sie ist aber überdiess eine
symmetrische Fläche. Denn wenn man die übereinanderliegenden
Puncte der beiden Flächenseiten vertauscht, so erfährt
die Gesammtfläche eine conforme Abbildung auf sich
selbst mit Umlegung der Winkel. Die Randcurven sind
dabei die Uebergangscurven. Zugleich aber gewinnt unsere
Eintheilung der symmetrischen Flächen in zweierlei Arten eine
wichtige und durchschlagende Bedeutung. Die gewöhnlichen
berandeten Flächen, bei denen man zwei Flächenseiten unterscheiden
kann, entsprechen offenbar der ersten Art. Der
zweiten Art aber correspondiren die Doppelflächen, bei denen
man von einer Flächenseite durch continuirliches Fortschreiten
über die Fläche hin zur anderen gelangen kann. Auch der
Fall ist nicht auszuschliessen (wie bereits angedeutet), dass
die Doppelfläche überhaupt keine Randcurve besitzen mag.
Wir haben dann eine symmetrische Fläche ohne Uebergangscurve
vor uns.
Ich betrachte nunmehr der Reihe nach die verschiedenen
auseinanderzuhaltenden Fälle.
1) Sei zuvörderst eine einfach berandete, einfach zusammenhängende
Fläche gegeben. Eine solche Fläche erscheint für
uns als eine geschlossene Fläche 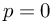 , welche unter Auftreten
einer Uebergangscurve symmetrisch auf sich selbst
bezogen ist. Wir finden also, dass zwei solche Flächen sich
allemal durch Abbildung der einen oder der anderen Art conform
, welche unter Auftreten
einer Uebergangscurve symmetrisch auf sich selbst
bezogen ist. Wir finden also, dass zwei solche Flächen sich
allemal durch Abbildung der einen oder der anderen Art conform
<TEI>
<text>
<body>
<div n="1">
<div>
<p><pb facs="#f0087" n="79"/><hi rendition="#i">Man fasse nämlich die beiden Seiten der berandeten
Fläche als Polyederflächen auf, welche längs der
Randcurve (also durchweg unter einem Winkel von 360 Grad)
zusammenstossen und behandele nunmehr statt der ursprünglichen
berandeten Fläche die aus beiden Seiten zusammengesetzte
Gesammtfläche.</hi><note place="foot"><p>Ich drücke mich im Texte der Kürze halber so aus, als wenn
die ursprüngliche Fläche eine zweiseitige Fläche gewesen wäre,
während doch nicht ausgeschlossen sein soll, dass sie eine Doppelfläche
ist.</p></note> Diese Gesammtfläche ist dann in der
That eine geschlossene Fläche. Sie ist aber überdiess eine <hi rendition="#i">symmetrische</hi> Fläche. Denn wenn man die übereinanderliegenden
Puncte der beiden Flächenseiten vertauscht, so erfährt
die Gesammtfläche eine conforme Abbildung auf sich
selbst mit Umlegung der Winkel. Die Randcurven sind
dabei die Uebergangscurven. <hi rendition="#i">Zugleich aber gewinnt unsere
Eintheilung der symmetrischen Flächen in zweierlei Arten eine
wichtige und durchschlagende Bedeutung.</hi> Die gewöhnlichen
berandeten Flächen, bei denen man zwei Flächenseiten unterscheiden
kann, entsprechen offenbar der ersten Art. Der
zweiten Art aber correspondiren die <hi rendition="#i">Doppelflächen</hi>, bei denen
man von einer Flächenseite durch continuirliches Fortschreiten
über die Fläche hin zur anderen gelangen kann. Auch der
Fall ist nicht auszuschliessen (wie bereits angedeutet), dass
die Doppelfläche überhaupt keine Randcurve besitzen mag. <hi rendition="#i">Wir haben dann eine symmetrische Fläche ohne Uebergangscurve
vor uns.</hi></p>
<p>Ich betrachte nunmehr der Reihe nach die verschiedenen
auseinanderzuhaltenden Fälle.</p>
<p>1) <hi rendition="#i">Sei zuvörderst eine einfach berandete, einfach zusammenhängende
Fläche gegeben.</hi> Eine solche Fläche erscheint für
uns als eine geschlossene Fläche <formula notation="TeX">p = 0</formula>, welche unter Auftreten
einer Uebergangscurve symmetrisch auf sich selbst
bezogen ist. Wir finden also, <hi rendition="#i">dass zwei solche Flächen sich
allemal durch Abbildung der einen oder der anderen Art conform
</hi></p>
</div>
</div>
</body>
</text>
</TEI>
[79/0087]
Man fasse nämlich die beiden Seiten der berandeten Fläche als Polyederflächen auf, welche längs der Randcurve (also durchweg unter einem Winkel von 360 Grad) zusammenstossen und behandele nunmehr statt der ursprünglichen berandeten Fläche die aus beiden Seiten zusammengesetzte Gesammtfläche. Diese Gesammtfläche ist dann in der That eine geschlossene Fläche. Sie ist aber überdiess eine symmetrische Fläche. Denn wenn man die übereinanderliegenden Puncte der beiden Flächenseiten vertauscht, so erfährt die Gesammtfläche eine conforme Abbildung auf sich selbst mit Umlegung der Winkel. Die Randcurven sind dabei die Uebergangscurven. Zugleich aber gewinnt unsere Eintheilung der symmetrischen Flächen in zweierlei Arten eine wichtige und durchschlagende Bedeutung. Die gewöhnlichen berandeten Flächen, bei denen man zwei Flächenseiten unterscheiden kann, entsprechen offenbar der ersten Art. Der zweiten Art aber correspondiren die Doppelflächen, bei denen man von einer Flächenseite durch continuirliches Fortschreiten über die Fläche hin zur anderen gelangen kann. Auch der Fall ist nicht auszuschliessen (wie bereits angedeutet), dass die Doppelfläche überhaupt keine Randcurve besitzen mag. Wir haben dann eine symmetrische Fläche ohne Uebergangscurve vor uns.
Ich betrachte nunmehr der Reihe nach die verschiedenen auseinanderzuhaltenden Fälle.
1) Sei zuvörderst eine einfach berandete, einfach zusammenhängende Fläche gegeben. Eine solche Fläche erscheint für uns als eine geschlossene Fläche [FORMEL], welche unter Auftreten einer Uebergangscurve symmetrisch auf sich selbst bezogen ist. Wir finden also, dass zwei solche Flächen sich allemal durch Abbildung der einen oder der anderen Art conform
Ich drücke mich im Texte der Kürze halber so aus, als wenn die ursprüngliche Fläche eine zweiseitige Fläche gewesen wäre, während doch nicht ausgeschlossen sein soll, dass sie eine Doppelfläche ist.
�



