x = z - 1/2 a
so ist x2 = z2 - az + 1/4 aa
+ ax = + az - 1/2 aa
z2 - 1/4aa = yy/ wie im ersten Falle.
III. Es sey
xx + ax = yy + by. Nehmet
das andere Glied
ax weg. Setzet zu dem
Ende
x = z -1/2 aso ist
x2 = z2 - az + 1/4 aa
+ ax = + az - 1/2 aa
z2 - 1/4aa = yy + by.Nehmet auf gleiche Weise
by weg. Zu
dem Ende setzet
y = v - 1/2bso ist
y2 = v2 - bv + 1/4b2
+ by = + bv - 1/2 b2
z2 - 1/4aa = v2 - 1/4 b2
z2 + 1/4bb - 1/4 aa = v2Setzet endlich
V (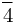 aa - 1/4bb) = c/
aa - 1/4bb) = c/ so ist
z2 - cc = v2/ wie in dem ersten
Falle.
IV. Es sey xx + xy = ab - cy. Schaffet
das andere Glied xy ab. Setzet zu dem
Ende
x
O 4
x = z - ½ a
ſo iſt x2 = z2 - az + ¼ aa
+ ax = + az - ½ aa
z2 - ¼aa = yy/ wie im erſten Falle.
III. Es ſey
xx + ax = yy + by. Nehmet
das andere Glied
ax weg. Setzet zu dem
Ende
x = z -½ aſo iſt
x2 = z2 - az + ¼ aa
+ ax = + az - ½ aa
z2 - ¼aa = yy + by.Nehmet auf gleiche Weiſe
by weg. Zu
dem Ende ſetzet
y = v - ½bſo iſt
y2 = v2 - bv + ¼b2
+ by = + bv - ½ b2
z2 - ¼aa = v2 - ¼ b2
z2 + ¼bb - ¼ aa = v2Setzet endlich
V (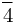 aa - ¼bb) = c/
aa - ¼bb) = c/ ſo iſt
z2 - cc = v2/ wie in dem erſten
Falle.
IV. Es ſey xx + xy = ab - cy. Schaffet
das andere Glied xy ab. Setzet zu dem
Ende
x
O 4
<TEI>
<text>
<body>
<div n="1">
<div n="2">
<div n="3">
<div n="4">
<div n="5">
<list>
<item><pb facs="#f0217" n="215"/><fw place="top" type="header"><hi rendition="#b">der Algebra.</hi></fw><lb/><hi rendition="#aq"><hi rendition="#u"><hi rendition="#i">x = z</hi> - ½ <hi rendition="#i">a</hi></hi></hi><lb/>
ſo iſt <hi rendition="#aq"><hi rendition="#i">x</hi><hi rendition="#sup">2</hi> = <hi rendition="#i">z</hi><hi rendition="#sup">2</hi> - <hi rendition="#i">az</hi> + ¼ <hi rendition="#i">aa</hi><lb/><hi rendition="#u">+ <hi rendition="#i">ax = + az</hi> - ½ <hi rendition="#i">aa</hi></hi><lb/><hi rendition="#i">z</hi>2 - ¼<hi rendition="#i">aa = yy/</hi></hi> wie im erſten Falle.</item><lb/>
<item><hi rendition="#aq">III.</hi> Es ſey <hi rendition="#aq"><hi rendition="#i">xx + ax = yy + by.</hi></hi> Nehmet<lb/>
das andere Glied <hi rendition="#aq"><hi rendition="#i">ax</hi></hi> weg. Setzet zu dem<lb/>
Ende<lb/><hi rendition="#aq"><hi rendition="#u"><hi rendition="#i">x = z</hi> -½ <hi rendition="#i">a</hi></hi></hi><lb/>
ſo iſt <hi rendition="#aq"><hi rendition="#i">x</hi><hi rendition="#sup">2</hi> = <hi rendition="#i">z</hi><hi rendition="#sup">2</hi> - <hi rendition="#i">az</hi> + ¼ <hi rendition="#i">aa</hi><lb/><hi rendition="#u">+ <hi rendition="#i">ax = + az</hi> - ½ <hi rendition="#i">aa</hi></hi><lb/><hi rendition="#i">z</hi><hi rendition="#sup">2</hi> - ¼<hi rendition="#i">aa = yy + by.</hi></hi><lb/>
Nehmet auf gleiche Weiſe <hi rendition="#aq"><hi rendition="#i">by</hi></hi> weg. Zu<lb/>
dem Ende ſetzet<lb/><hi rendition="#aq"><hi rendition="#u"><hi rendition="#i">y = v</hi> - ½<hi rendition="#i">b</hi></hi></hi><lb/>
ſo iſt <hi rendition="#aq"><hi rendition="#i">y</hi><hi rendition="#sup">2</hi> = <hi rendition="#i">v</hi><hi rendition="#sup">2</hi> - <hi rendition="#i">bv</hi> + ¼<hi rendition="#i">b</hi>2<lb/><hi rendition="#u">+ <hi rendition="#i">by = + bv</hi> - ½ <hi rendition="#i">b</hi><hi rendition="#sup">2</hi><lb/><hi rendition="#i">z</hi><hi rendition="#sup">2</hi> - ¼<hi rendition="#i">aa = v</hi>2 - ¼ <hi rendition="#i">b</hi><hi rendition="#sup">2</hi></hi><lb/><hi rendition="#i">z</hi><hi rendition="#sub">2</hi> + ¼<hi rendition="#i">bb</hi> - ¼ <hi rendition="#i">aa = v</hi>2</hi><lb/>
Setzet endlich <hi rendition="#aq">V (<formula notation="TeX">\frac {}{4}</formula> <hi rendition="#i">aa</hi> - ¼<hi rendition="#i">bb</hi>) = <hi rendition="#i">c/</hi></hi> ſo iſt<lb/><hi rendition="#aq"><hi rendition="#i">z</hi>2 - <hi rendition="#i">cc = v</hi>2/</hi> wie in dem erſten<lb/>
Falle.</item><lb/>
<item><hi rendition="#aq">IV.</hi> Es ſey <hi rendition="#aq"><hi rendition="#i">xx + xy = ab - cy.</hi></hi> Schaffet<lb/>
das andere Glied <hi rendition="#aq"><hi rendition="#i">xy</hi></hi> ab. Setzet zu dem<lb/>
Ende<lb/>
<fw place="bottom" type="sig">O 4</fw><fw place="bottom" type="catch"><hi rendition="#aq"><hi rendition="#i">x</hi></hi></fw><lb/></item>
</list>
</div>
</div>
</div>
</div>
</div>
</body>
</text>
</TEI>
[215/0217]
der Algebra.
x = z - ½ a
ſo iſt x2 = z2 - az + ¼ aa
+ ax = + az - ½ aa
z2 - ¼aa = yy/ wie im erſten Falle.
III. Es ſey xx + ax = yy + by. Nehmet
das andere Glied ax weg. Setzet zu dem
Ende
x = z -½ a
ſo iſt x2 = z2 - az + ¼ aa
+ ax = + az - ½ aa
z2 - ¼aa = yy + by.
Nehmet auf gleiche Weiſe by weg. Zu
dem Ende ſetzet
y = v - ½b
ſo iſt y2 = v2 - bv + ¼b2
+ by = + bv - ½ b2
z2 - ¼aa = v2 - ¼ b2
z2 + ¼bb - ¼ aa = v2
Setzet endlich V ([FORMEL] aa - ¼bb) = c/ ſo iſt
z2 - cc = v2/ wie in dem erſten
Falle.
IV. Es ſey xx + xy = ab - cy. Schaffet
das andere Glied xy ab. Setzet zu dem
Ende
x
O 4�



